“Mimblewimble” 是国外著名影视剧《哈利·波特》中来防范黑魔法诅咒用的一种保护性口诀,正因为它是如此的奇妙,所以也用它作为命名,意图在区块链中施展一种“神奇”的“魔法”可以隐藏交易内容,但是同时又可以验证交易的正确性。
刚才我们说了mimblewimble的由来,那mimblewimble真实的技术本质又是什么呢?
首先,我们要知道mimblewimble底层都是由密码学构成,它应用了密码学中的椭圆曲线加密技术,构造perdersen commitment(皮德森承诺),然后通过一种协议完成一笔隐藏交易,那么我们先大概学习下椭圆曲线:
椭圆曲线:
椭圆曲线名称名称由来是因为椭圆的周长公式很像这种曲线方程,所以称为椭圆曲线,如下图就是一种简单标准的椭圆曲线,方程式为:y**2 = x**3 - 7x + 10
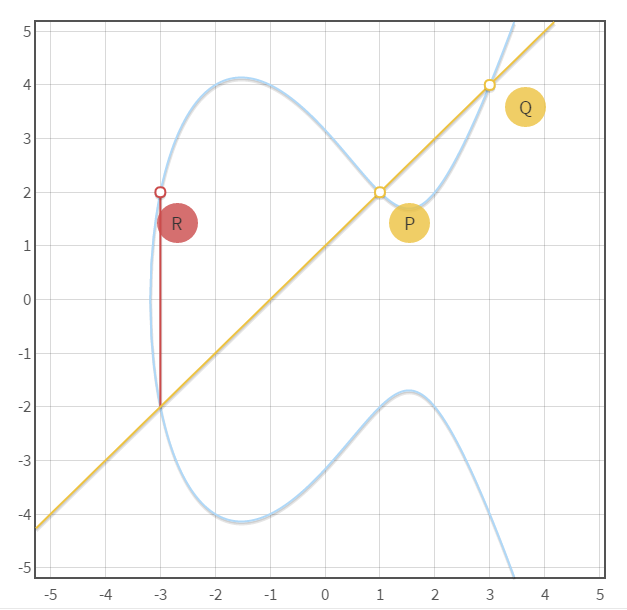
在此基础上我们定义一种“+”运算,即过椭圆曲线上的两点,构成一条直线,直线又会相较于椭圆曲线第三个点,对第三个点做垂线,垂线又会与椭圆曲线相较于另一点,该点便为两点相加之和。
例如上图所示:椭圆曲线上两点Q,P可做一条直线,直线与椭圆曲线相交于一点,过此点又做垂线,相交于椭圆曲线上的另一点R点,整个过程是运算一种加法: Q + P = R
(实际过程是在mod n的情况下进行的,即n素数域内,因为如果不在素数域里处理,加法生成的很多点,非整数,不利于处理,椭圆曲线的安全难度也不够,该部分就不详解了,想深入学习者,可以自行查找资料,本章节主要是为了介绍椭圆曲线的核心思想)
在此基础上,我们可以做一种新的乘法扩展,譬如下图,Q+Q我们可以写作2*Q
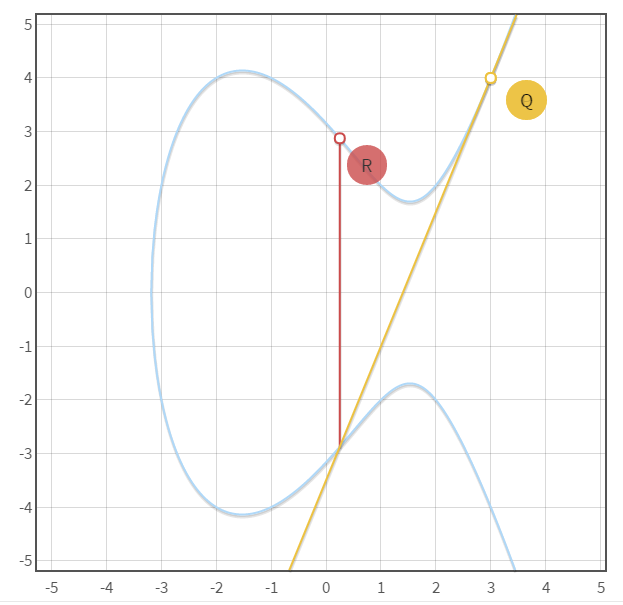
如上图,过椭圆曲线上的Q点做切线,即Q+Q=R我们可以写作2*Q=R ,拓展:4Q=R+R,…,8Q=4Q+4Q,…,16Q=8Q+8Q,…,32Q=16Q+16Q,…,64Q=32Q+32*Q,…,等
这时,就可以发现难点,假设我们经过x次Q点相加,即x*Q等于椭圆曲线上的一点假设为M,很容易算出M(如果x很大时,每次都是如上拓展叠加上去),但是如果我们不知道x,从Q,M反推x,几乎是不可能的(该问题和求对数问题是同价的,加上是在mod下计算的,也即离散的,所以该难题也被称作椭圆曲线上的离散对数问题):
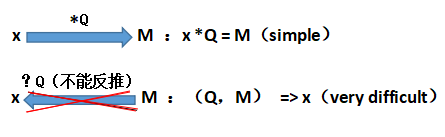
由此,我们把x作为椭圆曲线加密的私钥,M作为公钥,只能私钥推出公钥,公钥推不出私钥(如果用暴力破解,但是当x很大很大时,比如以太坊私钥的长度256bit,除非量子计算机的出世,不然就经典计算机的运算速度是毫无可能的)
皮德森承诺(perdersen commitment):
在我们讲完了椭圆曲线是怎样构造公私钥的之后,我们就要把该算法应用到皮德森承诺,在mimblewimble中我们需要隐藏金额v还有该承诺对应的私钥r,诸如 :
C = r * G + v * H
(这里的G,H都是椭圆曲线上的公开的点,r,v是该承诺的私钥(也可叫做致盲因子)和金额,也可以分别当为如上章节所讲的G,H两个点各自叠加的次数,你可以通过r,v推出C,但是从C获取不了任何信息)
如上形式的,就称C为一个perdersen承诺,其作用是为了隐藏r ,v两个值,因为椭圆曲线上的难题,你没法反推出r,v,所以在只有你拥有r,v两个值的时候,你才能通过perdersen 承诺花这笔价值为v的钱。
在mimblewimble系统中,交易的输入输出就是这些perdersen承诺,即一个输入对应一个perdersen承诺(所以在这个系统中也就没有了地址,具有了一定的隐私性),但是如何来使整个交易成立,并且可以验证交易的正确性,在接下来的一章节,我们再详细讲解。